Graph Algorithms in Java

Graph algorithms form the backbone of modern software development, powering everything from social networks and navigation systems to recommendation engines and network security. In Java, implementing efficient graph algorithms is crucial for building scalable applications that can handle complex relationships between data points.

A graph is a non-linear data structure consisting of vertices (nodes) connected by edges, making it perfect for representing relationships, networks, and hierarchical structures that traditional linear data structures cannot efficiently handle.

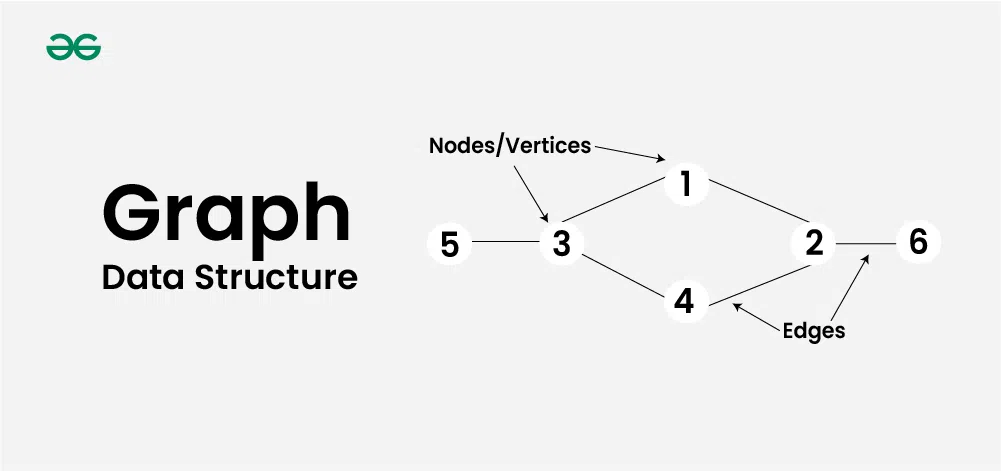Source: GeeksforGeeks - Graph Data Structure Visualization

Why Graph Algorithms Matter

Real-World Applications

Graph algorithms solve critical problems across industries:

• Social Networks: Finding friends-of-friends, community detection, influence analysis
• Navigation Systems: Shortest path calculation, route optimization, traffic analysis
• Recommendation Systems: User-item relationships, collaborative filtering
• Network Security: Anomaly detection, vulnerability assessment
• Dependency Management: Build systems, package managers, task scheduling
• Web Search: PageRank algorithm, link analysis, content discovery

Performance Impact

Choosing the right graph algorithm can dramatically impact application performance. For instance, using Dijkstra’s algorithm for shortest path problems offers O((V + E) log V) complexity, while a naive approach might result in exponential time complexity.

Core Concepts

Graph Terminology

Before diving into implementations, let’s establish key terminology:

• Vertex/Node: Individual data points in the graph
• Edge: Connection between two vertices
• Directed Graph: Edges have direction (one-way connections)
• Undirected Graph: Edges are bidirectional
• Weighted Graph: Edges have associated costs/weights
• Degree: Number of edges connected to a vertex

Graph Representations

Java offers two primary ways to represent graphs:

1. Adjacency Matrix

// Simple adjacency matrix representation
public class GraphMatrix {
    private int[][] adjMatrix;
    private int numVertices;
    
    public GraphMatrix(int numVertices) {
        this.numVertices = numVertices;
        this.adjMatrix = new int[numVertices][numVertices];
    }
    
    // Add edge between vertices u and v
    public void addEdge(int u, int v) {
        adjMatrix[u][v] = 1; // For unweighted graph
        adjMatrix[v][u] = 1; // For undirected graph
    }
    
    // Check if edge exists
    public boolean hasEdge(int u, int v) {
        return adjMatrix[u][v] == 1;
    }
}

2. Adjacency List (Recommended)

import java.util.*;

public class Graph {
    private Map<Integer, List<Integer>> adjList;
    private boolean isDirected;
    
    public Graph(boolean isDirected) {
        this.adjList = new HashMap<>();
        this.isDirected = isDirected;
    }
    
    // Add vertex to the graph
    public void addVertex(int vertex) {
        adjList.putIfAbsent(vertex, new ArrayList<>());
    }
    
    // Add edge between vertices
    public void addEdge(int source, int destination) {
        // Add vertices if they don't exist
        addVertex(source);
        addVertex(destination);
        
        // Add edge from source to destination
        adjList.get(source).add(destination);
        
        // For undirected graph, add reverse edge
        if (!isDirected) {
            adjList.get(destination).add(source);
        }
    }
    
    // Get neighbors of a vertex
    public List<Integer> getNeighbors(int vertex) {
        return adjList.getOrDefault(vertex, new ArrayList<>());
    }
    
    // Get all vertices
    public Set<Integer> getVertices() {
        return adjList.keySet();
    }
}

Code Walkthrough

Breadth-First Search (BFS)

BFS explores vertices level by level, making it ideal for finding shortest paths in unweighted graphs.

Source: GeeksforGeeks - BFS vs DFS Comparison

import java.util.*;

public class BFSTraversal {
    
    /**
     * Performs BFS traversal starting from a given source vertex
     * Time Complexity: O(V + E) where V = vertices, E = edges
     * Space Complexity: O(V) for the queue and visited set
     */
    public List<Integer> bfs(Graph graph, int startVertex) {
        List<Integer> result = new ArrayList<>();
        Set<Integer> visited = new HashSet<>();
        Queue<Integer> queue = new LinkedList<>();
        
        // Start from the source vertex
        queue.offer(startVertex);
        visited.add(startVertex);
        
        while (!queue.isEmpty()) {
            int currentVertex = queue.poll();
            result.add(currentVertex);
            
            // Visit all unvisited neighbors
            for (int neighbor : graph.getNeighbors(currentVertex)) {
                if (!visited.contains(neighbor)) {
                    visited.add(neighbor);
                    queue.offer(neighbor);
                }
            }
        }
        
        return result;
    }
    
    /**
     * Finds shortest path between two vertices using BFS
     * Returns the path as a list of vertices
     */
    public List<Integer> shortestPath(Graph graph, int start, int end) {
        if (start == end) {
            return Arrays.asList(start);
        }
        
        Map<Integer, Integer> parent = new HashMap<>();
        Set<Integer> visited = new HashSet<>();
        Queue<Integer> queue = new LinkedList<>();
        
        queue.offer(start);
        visited.add(start);
        parent.put(start, null);
        
        while (!queue.isEmpty()) {
            int current = queue.poll();
            
            for (int neighbor : graph.getNeighbors(current)) {
                if (!visited.contains(neighbor)) {
                    visited.add(neighbor);
                    parent.put(neighbor, current);
                    queue.offer(neighbor);
                    
                    // Found the target
                    if (neighbor == end) {
                        return reconstructPath(parent, start, end);
                    }
                }
            }
        }
        
        return new ArrayList<>(); // No path found
    }
    
    private List<Integer> reconstructPath(Map<Integer, Integer> parent, 
                                        int start, int end) {
        List<Integer> path = new ArrayList<>();
        Integer current = end;
        
        while (current != null) {
            path.add(current);
            current = parent.get(current);
        }
        
        Collections.reverse(path);
        return path;
    }
}

Depth-First Search (DFS)

DFS explores as far as possible along each branch before backtracking, useful for topological sorting and cycle detection.

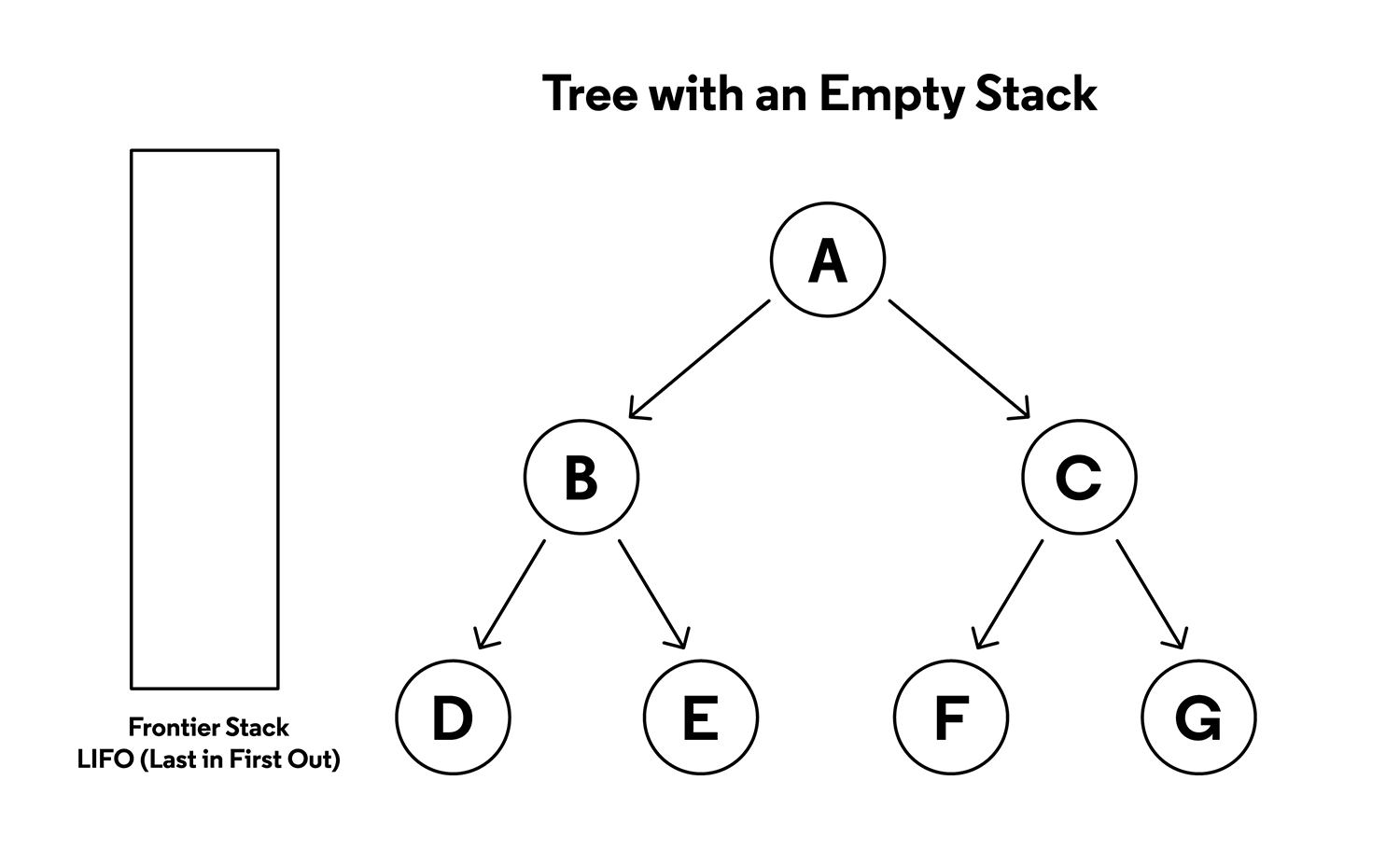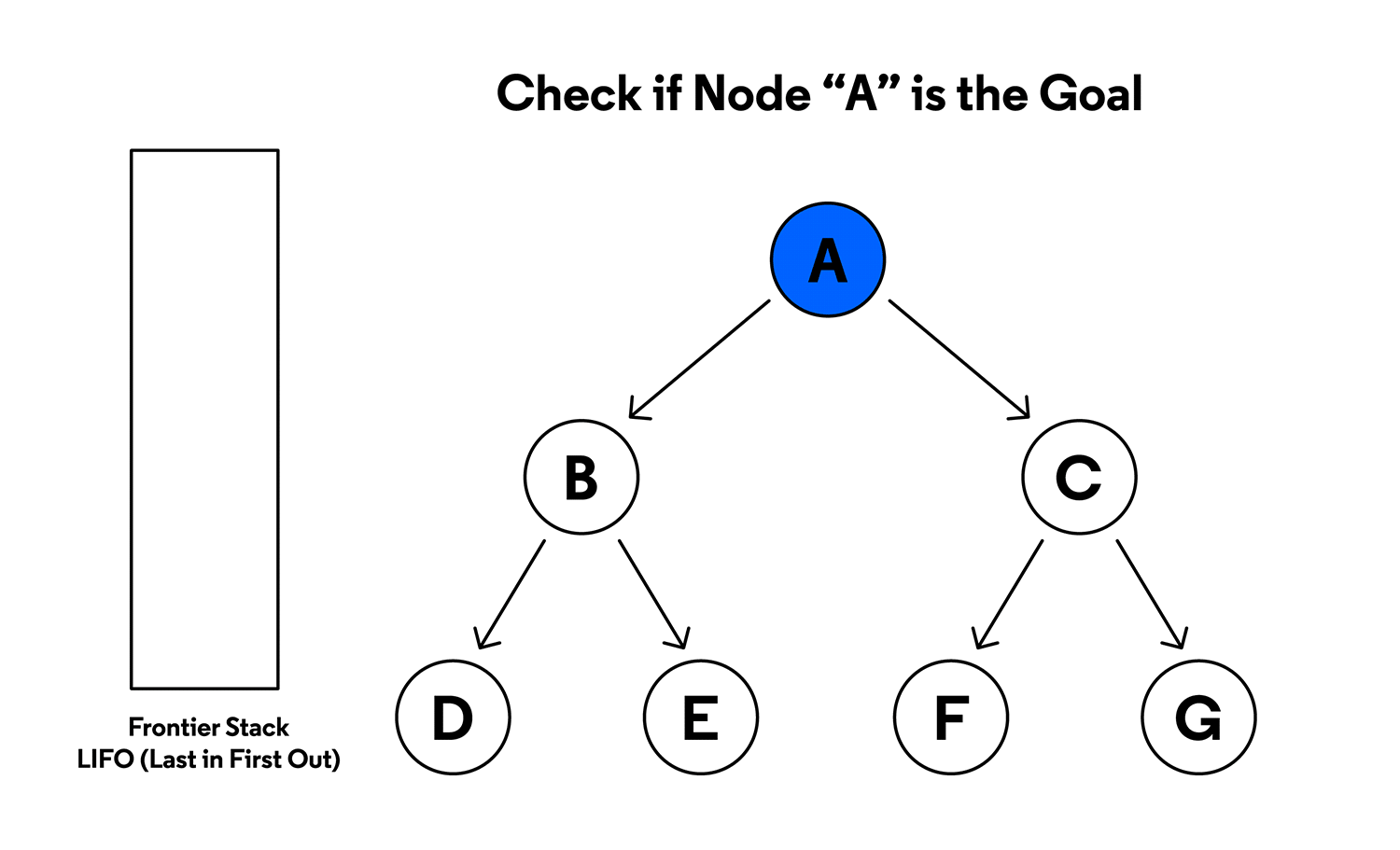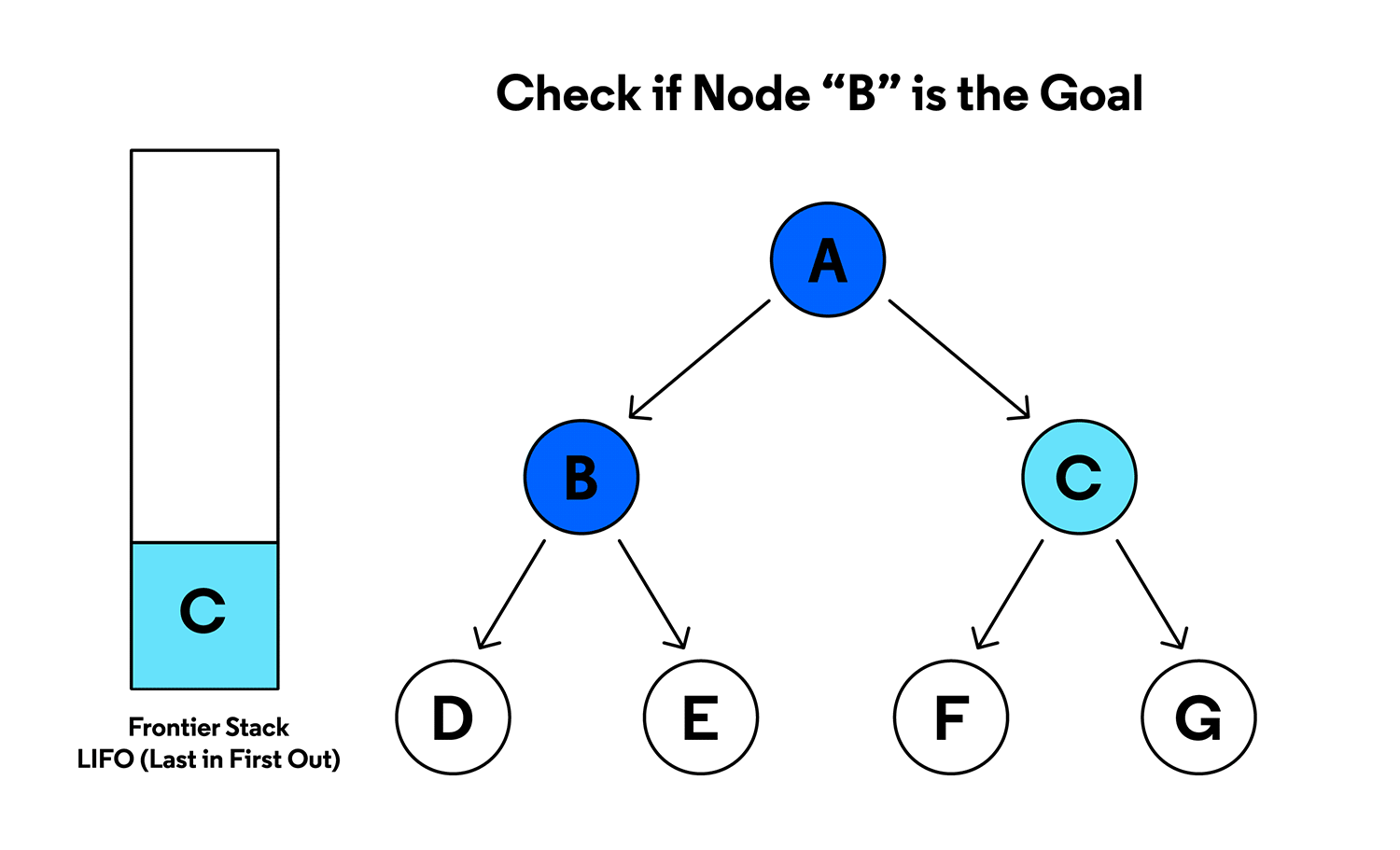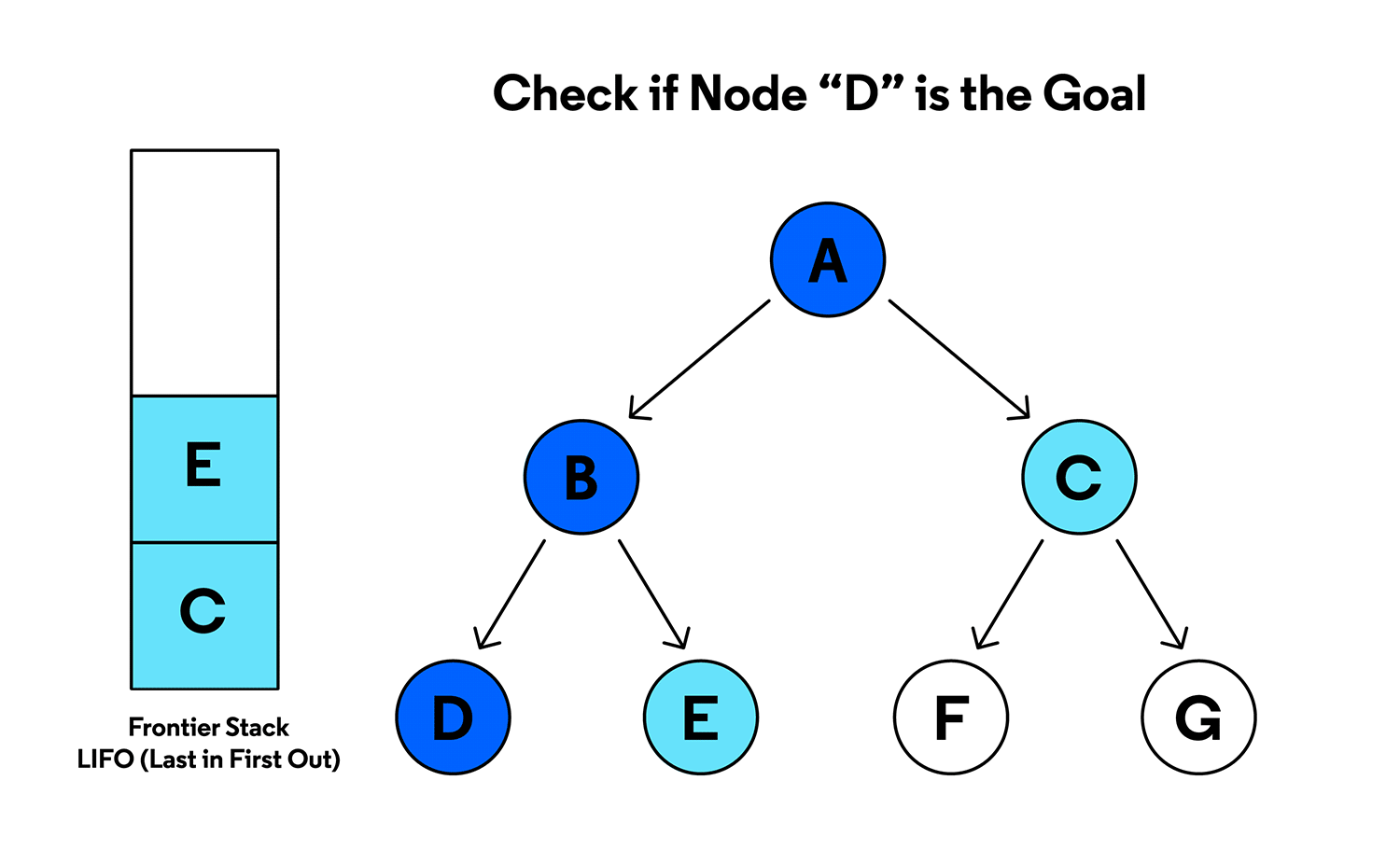Source: Codecademy - Depth-First Search Visualization

import java.util.*;

public class DFSTraversal {
    
    /**
     * Recursive DFS implementation
     * Time Complexity: O(V + E)
     * Space Complexity: O(V) for recursion stack
     */
    public List<Integer> dfsRecursive(Graph graph, int startVertex) {
        List<Integer> result = new ArrayList<>();
        Set<Integer> visited = new HashSet<>();
        dfsHelper(graph, startVertex, visited, result);
        return result;
    }
    
    private void dfsHelper(Graph graph, int vertex, Set<Integer> visited, 
                          List<Integer> result) {
        visited.add(vertex);
        result.add(vertex);
        
        // Visit all unvisited neighbors
        for (int neighbor : graph.getNeighbors(vertex)) {
            if (!visited.contains(neighbor)) {
                dfsHelper(graph, neighbor, visited, result);
            }
        }
    }
    
    /**
     * Iterative DFS implementation using stack
     * More memory efficient than recursive approach
     */
    public List<Integer> dfsIterative(Graph graph, int startVertex) {
        List<Integer> result = new ArrayList<>();
        Set<Integer> visited = new HashSet<>();
        Stack<Integer> stack = new Stack<>();
        
        stack.push(startVertex);
        
        while (!stack.isEmpty()) {
            int current = stack.pop();
            
            if (!visited.contains(current)) {
                visited.add(current);
                result.add(current);
                
                // Add neighbors to stack (in reverse order for consistent traversal)
                List<Integer> neighbors = graph.getNeighbors(current);
                for (int i = neighbors.size() - 1; i >= 0; i--) {
                    int neighbor = neighbors.get(i);
                    if (!visited.contains(neighbor)) {
                        stack.push(neighbor);
                    }
                }
            }
        }
        
        return result;
    }
    
    /**
     * Detects cycles in a directed graph using DFS
     */
    public boolean hasCycle(Graph graph) {
        Set<Integer> visited = new HashSet<>();
        Set<Integer> recursionStack = new HashSet<>();
        
        for (int vertex : graph.getVertices()) {
            if (!visited.contains(vertex)) {
                if (hasCycleHelper(graph, vertex, visited, recursionStack)) {
                    return true;
                }
            }
        }
        return false;
    }
    
    private boolean hasCycleHelper(Graph graph, int vertex, Set<Integer> visited, 
                                  Set<Integer> recursionStack) {
        visited.add(vertex);
        recursionStack.add(vertex);
        
        for (int neighbor : graph.getNeighbors(vertex)) {
            if (!visited.contains(neighbor)) {
                if (hasCycleHelper(graph, neighbor, visited, recursionStack)) {
                    return true;
                }
            } else if (recursionStack.contains(neighbor)) {
                return true; // Back edge found - cycle detected
            }
        }
        
        recursionStack.remove(vertex); // Remove from recursion stack
        return false;
    }
}

Weighted Graph Implementation

For more complex algorithms like Dijkstra’s shortest path, we need weighted graphs:

import java.util.*;

public class WeightedGraph {
    // Inner class to represent weighted edges
    public static class Edge {
        int destination;
        int weight;
        
        public Edge(int destination, int weight) {
            this.destination = destination;
            this.weight = weight;
        }
        
        @Override
        public String toString() {
            return "(" + destination + ", " + weight + ")";
        }
    }
    
    private Map<Integer, List<Edge>> adjList;
    private boolean isDirected;
    
    public WeightedGraph(boolean isDirected) {
        this.adjList = new HashMap<>();
        this.isDirected = isDirected;
    }
    
    public void addVertex(int vertex) {
        adjList.putIfAbsent(vertex, new ArrayList<>());
    }
    
    public void addEdge(int source, int destination, int weight) {
        addVertex(source);
        addVertex(destination);
        
        adjList.get(source).add(new Edge(destination, weight));
        
        if (!isDirected) {
            adjList.get(destination).add(new Edge(source, weight));
        }
    }
    
    public List<Edge> getNeighbors(int vertex) {
        return adjList.getOrDefault(vertex, new ArrayList<>());
    }
    
    /**
     * Dijkstra's shortest path algorithm
     * Time Complexity: O((V + E) log V) with priority queue
     */
    public Map<Integer, Integer> dijkstra(int startVertex) {
        Map<Integer, Integer> distances = new HashMap<>();
        PriorityQueue<Edge> pq = new PriorityQueue<>(
            Comparator.comparingInt(e -> e.weight)
        );
        Set<Integer> visited = new HashSet<>();
        
        // Initialize distances
        for (int vertex : adjList.keySet()) {
            distances.put(vertex, Integer.MAX_VALUE);
        }
        distances.put(startVertex, 0);
        
        pq.offer(new Edge(startVertex, 0));
        
        while (!pq.isEmpty()) {
            Edge current = pq.poll();
            int currentVertex = current.destination;
            
            if (visited.contains(currentVertex)) {
                continue;
            }
            
            visited.add(currentVertex);
            
            for (Edge edge : getNeighbors(currentVertex)) {
                int neighbor = edge.destination;
                int newDistance = distances.get(currentVertex) + edge.weight;
                
                if (newDistance < distances.get(neighbor)) {
                    distances.put(neighbor, newDistance);
                    pq.offer(new Edge(neighbor, newDistance));
                }
            }
        }
        
        return distances;
    }
}

Common Mistakes

1. Not Handling Disconnected Components

// ❌ Wrong: Only explores one component
public void wrongTraversal(Graph graph, int start) {
    dfs(graph, start);
}

// ✅ Correct: Handles all components
public void correctTraversal(Graph graph) {
    Set<Integer> globalVisited = new HashSet<>();
    
    for (int vertex : graph.getVertices()) {
        if (!globalVisited.contains(vertex)) {
            List<Integer> component = dfs(graph, vertex);
            globalVisited.addAll(component);
            // Process this component
        }
    }
}

2. Memory Leaks in Large Graphs

// ❌ Wrong: Keeping unnecessary references
public class BadGraphProcessor {
    private List<Integer> allResults = new ArrayList<>(); // Grows indefinitely
    
    public void processGraph(Graph graph) {
        for (int vertex : graph.getVertices()) {
            allResults.addAll(bfs(graph, vertex)); // Memory leak!
        }
    }
}

// ✅ Correct: Process and clear
public class GoodGraphProcessor {
    public void processGraph(Graph graph) {
        Set<Integer> visited = new HashSet<>();
        
        for (int vertex : graph.getVertices()) {
            if (!visited.contains(vertex)) {
                List<Integer> component = bfs(graph, vertex);
                visited.addAll(component);
                processComponent(component); // Process immediately
                // component goes out of scope - GC can collect it
            }
        }
    }
}

3. Incorrect Cycle Detection

// ❌ Wrong: Using visited set only (works for undirected, fails for directed)
public boolean wrongCycleDetection(Graph graph, int vertex, Set<Integer> visited) {
    visited.add(vertex);
    for (int neighbor : graph.getNeighbors(vertex)) {
        if (visited.contains(neighbor)) {
            return true; // This is wrong for directed graphs!
        }
    }
    return false;
}

// ✅ Correct: Using recursion stack for directed graphs
// (See the hasCycle implementation above)

4. Not Considering Thread Safety

// ❌ Wrong: Shared mutable state in concurrent environment
public class UnsafeGraph {
    private Set<Integer> visited = new HashSet<>(); // Shared state!
    
    public List<Integer> bfs(int start) {
        visited.clear(); // Race condition!
        // ... rest of BFS
    }
}

// ✅ Correct: Local state or proper synchronization
public class SafeGraph {
    public List<Integer> bfs(int start) {
        Set<Integer> visited = new HashSet<>(); // Local to method
        // ... rest of BFS
    }
}

Best Practices

1. Choose the Right Data Structure

• Adjacency List: Best for sparse graphs (fewer edges)
• Adjacency Matrix: Better for dense graphs or when you need O(1) edge lookup
• Edge List: Suitable for algorithms that iterate over all edges

2. Optimize for Your Use Case

// For frequently queried shortest paths, precompute distances
public class OptimizedGraph {
    private Map<Pair<Integer, Integer>, Integer> shortestPaths;
    
    // Precompute all-pairs shortest paths using Floyd-Warshall
    public void precomputeShortestPaths() {
        // Implementation here...
    }
    
    // O(1) lookup for shortest distance
    public int getShortestDistance(int from, int to) {
        return shortestPaths.get(new Pair<>(from, to));
    }
}

3. Handle Edge Cases Gracefully

public class RobustGraph {
    public List<Integer> safeBFS(Graph graph, int start) {
        // Validate inputs
        if (graph == null || !graph.getVertices().contains(start)) {
            return new ArrayList<>();
        }
        
        // Handle empty graph
        if (graph.getVertices().isEmpty()) {
            return new ArrayList<>();
        }
        
        return bfs(graph, start);
    }
}

4. Use Appropriate Collections

// ✅ Good: Use specific collections for better performance
Set<Integer> visited = new HashSet<>();        // O(1) contains()
Queue<Integer> queue = new ArrayDeque<>();     // Better than LinkedList
PriorityQueue<Edge> pq = new PriorityQueue<>(); // For Dijkstra's algorithm

5. Document Time and Space Complexity

/**
 * Performs topological sort using DFS
 * @param graph Directed Acyclic Graph (DAG)
 * @return Topologically sorted order of vertices
 * @throws IllegalArgumentException if graph contains cycles
 * @timeComplexity O(V + E)
 * @spaceComplexity O(V) for recursion stack and data structures
 */
public List<Integer> topologicalSort(Graph graph) {
    // Implementation...
}

6. Implement Builder Pattern for Complex Graphs

public class GraphBuilder {
    private Graph graph;
    
    public GraphBuilder directed() {
        graph = new Graph(true);
        return this;
    }
    
    public GraphBuilder undirected() {
        graph = new Graph(false);
        return this;
    }
    
    public GraphBuilder addEdge(int from, int to) {
        graph.addEdge(from, to);
        return this;
    }
    
    public Graph build() {
        return graph;
    }
}

// Usage
Graph socialNetwork = new GraphBuilder()
    .undirected()
    .addEdge(1, 2)
    .addEdge(2, 3)
    .addEdge(1, 3)
    .build();

Reference Materials

For deeper understanding and advanced implementations, I recommend these authoritative sources:

• GeeksforGeeks Graph Algorithms - Comprehensive tutorials with examples
• Stack Overflow Graph Implementation Discussion - Real-world implementation considerations
• The Complete Beginner’s Guide to Graph Theory - Theoretical foundation

Final Thoughts

Graph algorithms in Java are powerful tools that can solve complex real-world problems efficiently. The key to mastery lies in understanding when to use each algorithm and how to implement them correctly for your specific use case.

Start with the fundamental traversal algorithms (BFS and DFS) and gradually work your way up to more complex algorithms like Dijkstra’s shortest path, minimum spanning trees (Kruskal’s and Prim’s), and advanced topics like network flow algorithms.

Remember that choosing the right graph representation and being mindful of time and space complexity can make the difference between a scalable application and one that struggles under load. Practice implementing these algorithms from scratch, but also familiarize yourself with existing libraries like JGraphT for production use.

---